INTRODUCCIÓN

El orden y* el caos: estimula la imaginación y la creatividad.
El orden o** el caos: inhiben la imaginación y la creatividad, permitiendo a
algunos desarrollar un poder omnímodo para afectar las vidas de otros.

* y: el uno se fusiona con el otro.
** o: el uno excluye al otro.

Este Tractatus ofrece un nuevo, o desde hace mucho olvidado, juego de lenguaje. Lo ofrece sin recurrir a definiciones o explicaciones, sino más bien mostrando, como diciendo el nombre de las ideas y apuntándolas con el dedo. Invita a los observadores, principalmente con metáforas, a explorar nuevas formas de ver (entender) sus ambientes, y nuevas formas de expresar sus deseos e interacciones.

Nos parece fácil aceptar la descripción de todo fenómeno mediante procesos o redes de procesos. (Considérese fenómenos tales como el movimiento de una extremidad, la explosión de una estrella, los “choques” de “partículas” subatómicas, el “comienzo” del “universo” y sus subsiguientes transformaciones, etc.)

No nos parece tan fácil, sin embargo, aceptar que una red de procesos cerrada sobre sí misma pueda ella misma distinguirse, como observador, de un ambiente hecho presente por esta misma distinción. Además, considere: (1) que el ambiente distinguido contiene al observador (la red cerrada de procesos) y (2) que desde la perspectiva de este observador, esta distinción y las distinciones adicionales que resultan de la interacción entre este observador y su ambiente aparecen paradojales y lógicas. En otras palabras (paradójicamente), para el observador, todas las posibilidades se fusionan entre sí (por ejemplo, existe y no existe, dentro y fuera, rojo y azul y verde y … etc.) y (lógicamente), para el observador, las posibilidades se distinguen unas de otras (existe o no existe, dentro o fuera, rojo azul o verde o… etc.).

Los organismos vivos, con o sin un sistema nervioso, constituyen ejemplos de estas redes cerradas de procesos. Un sistema nervioso, también una red cerrada de procesos, interactúa con su medio ambiente a través de redes cerradas de procesos que involucran sus superficies sensorias y efectoras. Por lo tanto, el sistema nervioso interactúa con su medio ambiente (paradójicamente) dentro y fuera de él mismo y (lógicamente) dentro o fuera de él mismo.

Determinados en gran medida por su biología, uno o más observadores, razonando lógicamente, distinguen un mundo “allá fuera” hecho de objetos y sucesos, a los cuales les adjudican (mediante distinciones adicionales) posibilidades específicas como resultado de características y limitaciones perceptivas u otras, así como resultado de intentos de sociabilizar. Sin embargo, estos intentos también entrañan un avance hacia la trivialidad y un alejamiento del pensar y las paradojas. El conocimiento social, “objetivo” o “subjetivo”, tal como lo practican los lógicos, matemáticos, científicos, tecnólogos y otros, no proporciona excepción alguna. Un observador todavía puede acoger estos intentos, siempre que conduzcan a la conversación, evitando así la trivialización (instrucción) de uno por el otro y la de muchos por los pocos.

Dos o más observadores individuales no pueden distinguir un mundo común “allá fuera” a menos que alguna evidencia pueda convencerlos. Desde esta evidencia, el razonamiento lógico permite a los observadores humanos deducir inferencias sobre el mundo “allá fuera” que no se sostendrán a menos que alguna evidencia las apoye, reforzando así la distinción original de un mundo “allá fuera”. Como una nueva evidencia puede demostrar el error de evidencias previas, este proceso (evidencia, inferencias, nueva evidencia, nuevas inferencias…) no tiene fin, y puede cuestionar la distinción original de un mundo “allá fuera”, lo cual puede cuestionar el razonamiento lógico mismo, y sugerir en cambio un razonamiento paradójico.

Ningún observador “resuelve” o “explica” paradojas sin incurrir en una pérdida. Este punto de vista, como lo muestra el Tractatus, resulta esencial para aquellas sociedades que los humanos debieran desarrollar mediante la educación y el arte y la filosofía. El Tractatus no dice, ni enseña, ni explica qué educar; pero muestra la educación como si la estuviera indicando. También busca el origen de estas proposiciones irreverentes hasta la fuente misma de todas las proposiciones: la esencia paradojal del observador.

Si los humanos no sucumben a las deficiencias que ellos mismos se infligen, lo que sigue puede ayudarlos a verse (entenderse) y a ver (entender) las consecuencias de sólo razonar lógicamente, tal como lo hacen los lógicos, matemáticos, científicos, tecnólogos y otros; en busca de una verdad como si buscaran a un dios, traducen todo a su propio lenguaje y yerran miserablemente el blanco. Aquellos que practican estas disciplinas pronto olvidan o combaten su origen paradójico mucho porque aquellos humanos que se consideran “acomodados” y/o “contentos” y aquéllos que esperan alcanzar ese estado, acogen, exigen y/o se adaptan a un razonamiento lógico sin conflictos ni paradojas, forzando así un status quo.

De las lógicas a las paradojas

Consideremos una concatenación de palabras (una frase) y llamémosla una proposición (una declaración) inventada por uno o más observadores para aseverar o expresar algo dentro de un contexto dado.

Las proposiciones pueden tener distintos significados para diferentes grupos de uno o más observadores.

Razonando paradójicamente, un grupo de observadores puede encontrar significados comunes y tentativos para proposiciones a través de los juegos de lenguaje que definen sus formas de vida.

Razonando lógicamente, un grupo de observadores puede encontrar que algunas proposiciones no se refieren a sí mismas y que un observador o un grupo de ellos debe asignar o determinar sus valores lógicos (e.g., en una lógica de dos valores: verdadero, falso). Otros observadores pueden disentir y defender con argumentos, valores distintos.

Otras proposiciones se refieren a sí mismas (proposiciones auto-referentes) y determinan su propio valor lógico, por ejemplo, L: “La proposición L tiene aquí y ahora el valor verdadero”. Uno o más observadores pueden asignar uno u otro valor lógico (verdadero, falso) a L, y como L se refiere a sí misma no permite ningún argumento que dispute o que defienda esta elección.

Algunas proposiciones auto-referentes determinan su propio “valor lógico” como “verdadero y falso” y así impiden al observador la elección (distinción) entre “verdadero” o “falso”, como sucede con la proposición: P: “La proposición P tiene aquí y ahora el valor falso”.Si uno o más observadores, adoptando un razonamiento lógico, suponen que esta proposición tiene ahora el valor “verdadero”, pronto tendrán que aceptar, bajo esa suposición, su valor como “falso”. Si suponen el valor de la proposición como “falso”, pronto tendrán que aceptarlo como “verdadero”, y así en adelante. Para estos observadores los valores oscilan: verdadero, falso, verdadero, falso… cuando tratan de determinar un valor. Llamemos paradoja a esta proposición.

Desgraciadamente muchos autores que escriben sobre paradojas olvidan la auto-referencia y la fusión de diferentes posibilidades como aspectos esenciales de las paradojas, con la lamentable consecuencia de que muchas adivinanzas, acertijos, enigmas, etc., pasan por paradojas.

La paradoja no permite al observador asignar un valor “verdadero” o “falso” a la proposición excepto como parte de una oscilación, invitando así al observador a contemplar un razonamiento paradójico y fusionar los dos valores (todas las posibilidades en este caso) en “verdadero y falso”.

Razonando lógicamente, el observador sólo puede considerar ambos valores alternando en un tiempo y un espacio que resultan del observador contemplando la paradoja desde una perspectiva lógica.

Razonando paradójicamente, el observador fusiona “verdadero” o “falso” en “verdadero y falso” y por lo tanto, ni tiempo ni espacio ni oscilación resultan desde una perspectiva paradójica.

Con el razonamiento paradójico, sin embargo, el observador fusiona, sin conflicto, todas las posibilidades. Por lo tanto, con el razonamiento paradójico el observador también fusiona el razonamiento paradójico o lógico en razonamiento paradójico y lógico. En consecuencia, razonando paradójicamente, el observador también puede hacer distinciones tentativas en el tiempo y en el espacio.

En un bucle auto-referente de proposiciones, derivado de la proposición L, tal como el que sigue, todas las proposiciones tendrán uno u otro de los valores verdadero (V) o falso (F) dependiendo de cual valor elige el observador para una de las proposiciones, por ejemplo L1 (y no hay oscilación):

			t1	t2 ...
L1: “L2 tiene aquí y ahora el valor V.”			V(F)	V(F)…
L2: “L3 tiene aquí y ahora el valor V.”			V(F)	V(F)…
Ln: “L1 tiene aquí y ahora el valor V.”			V(F)	V(F)

Un bucle auto-referente de proposiciones, derivado de la proposición P, tal como el que sigue, no permitirá al observador asignar valores a ninguna de sus proposiciones ya que sus valores oscilarán lógicamente y se fusionarán paradójicamente para el observador como antes (Notemos que los valores ahora también varían a lo largo del bucle a medida que el observador, razonando lógicamente, determina los valores de cada proposición, haciendo la oscilación levemente más compleja que como se ve en la tabla que sigue):

			t1	t2	t3 ...
P1: “P2 tiene aquí y ahora el valor V.”			V	F	V ...
P2: “P3 tiene aquí y ahora el valor V.”			V	F	V ...
					...
Pn: “P1 tiene aquí y ahora el valor F.”			V	F	V ...

Como la proposición P, este bucle paradójico de proposiciones también sugiere el razonamiento paradójico al observador.

Si un observador toma una cinta de papel y une sus extremos, el observador forma un anillo con dos superficies (externa e interna) y dos bordes (derecho e izquierdo o arriba y abajo, dependiendo de cómo el observador sostiene el anillo). Asumiendo que cada superficie (o borde) del anillo corresponde a un valor (V, F), el observador puede ver el anillo entero como una metáfora del bucle de proposiciones derivado de L.

Si el observador gira 180 grados uno de los extremos antes de unirlo al otro, el observador forma una cinta de Möbius con una superficie y un borde (ver el anillo y la cinta de Möbius en la sección siguiente ). Tal como el bucle paradójico de proposiciones derivado de P que, para el observador que recorre el bucle de proposiciones, alterna lógicamente dos valores (en un tiempo y un espacio) y fusiona paradójicamente dos valores en uno (ni tiempo, ni espacio), para el observador que recorre la banda a lo largo, esta banda alterna lógicamente dos superficies (en un espacio y un tiempo) y fusiona paradójicamente dos superficies en una (ni tiempo, ni espacio); y alterna lógicamente dos bordes (en un espacio y un tiempo) y fusiona paradójicamente dos bordes en uno (ni tiempo, ni espacio). Notemos que la proposición n corresponde al giro y que cualquier número impar de giros mantiene la paradoja y que cualquier número par de giros la destruye, introduciendo una distinción.

Toroides lógicos y paradójicos

Si en lugar de una cinta, el observador tiene un tubo de sección poligonal que se cierra sobre sí mismo formando un toroide con 3, 4, 5, ... o n caras y cada cara representa una posibilidad (por ejemplo, un valor lógico en una lógica polivalente o una componente en una red cerrada de procesos y componentes) el observador tiene un toroide lógico del cual el observador puede formar un toroide paradójico (una cara y un borde) con el giro apropiado (360/3 =120 grados para 3 caras, 360/4=90 grados para 4 caras, 360/n para n caras (n posibilidades)).

Anillo y Cinta de Möbius: (2 caras <=> 1 cara; 2 bordes <=> 1 borde)

Toroides Lógicos y Toroides Paradójicos: (3 caras <=> 1 cara; 3 bordes <=> 1 borde)

Toroides Lógicos y Toroides Paradójicos: (4 caras <=> 1 cara; 4 bordes <=> 1 borde)

Para el observador que recorre a lo largo la cara resultante, el toroide paradójico alterna lógicamente n caras en un espacio y un tiempo y fusiona paradójicamente n caras en una eliminando tiempo y espacio. Razonando lógicamente, cada vez que el observador retorna al punto de partida después de cada vuelta alrededor del toroide paradójico el observador se encontrará sobre una cara diferente (y, paradójicamente, la misma cara). El toroide paradójico también sugiere un razonamiento paradójico al observador.

Consideremos ahora que un toroide lógico, como una metáfora para un conjunto de componentes (las caras del toroide) que no cambian (ni procesos, ni actividad), puede representar la estabilidad estática de las cosas no vivas.

Un toroide paradójico, sin embargo, como metáfora para un conjunto de componentes que sí cambian (debido a procesos) de una en otra, puede representar la estabilidad dinámica propia de todos los organismos vivos y de la actividad de sus sistemas nerviosos.

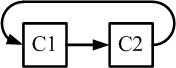
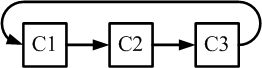
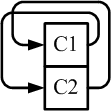
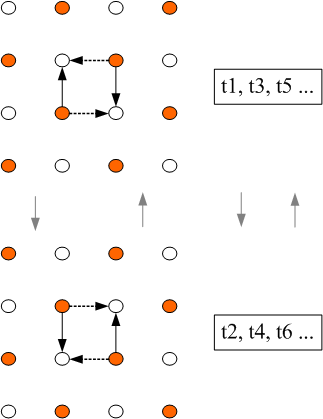
Razonando lógicamente, las redes cerradas de componentes que cambian se ven así (para 2 y 3 componentes):

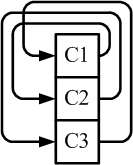Las flechas representan ahora componentes fusionándose, la auto-referencia y el giro (mejor representados por los toroides paradójicos correspondientes). Ni tiempo ni espacio resultan desde esta perspectiva.

De las paradojas a las lógicas

Hasta que sepamos más y mejor, podemos suponer que a medida que los infantes humanos se unen al mundo y a una sociedad, sus sistemas nerviosos, aún no avasallados por el entrenamiento y la instrucción, pero llenos de curiosidad, observan (exploran) sus alrededores y a si mismos contemplando todas las posibilidades, incluyendo las emociones y los sentimientos, no constreñidos por las limitaciones de un entramado lógico.

Desde esta suposición, contemplemos el observar (percibir) como resultado de la actividad de bucles cerrados de procesos que, cruzando las superficies sensoriales y motoras, residen dentro y fuera del sistema nervioso. Como esta actividad incluye todas las posibilidades, estos bucles deben parecerse a los toroides paradójicos discutidos en las páginas anteriores y juegan el papel de contextos paradójicos donde los observadores infantes, sin inhibiciones y razonando paradójicamente (el razonamiento lógico aún incipiente), hacen distinciones tentativas.

Una instrucción y un entrenamiento moderados pueden forzar a estos observadores a considerar sólo parte de sus toroides paradójicos (una parte que cada observador puede hacer coincidir con parte de los toroides de otros observadores) de modo que sólo emerge el razonamiento lógico. Por otro lado, una instrucción y un entrenamiento rigurosos y prolongados pueden forzar a los observadores a enderezar sus toroides paradójicos (para hacer un toroide lógico). Opuesto al primer caso que podría resultar reversible y que lleva a un observador algo flexible, el segundo caso podría resultar irreversible y llevar a un observador rígido que sólo considera el razonamiento lógico.

La mayoría de los observadores sucumben a estos métodos de coerción y abandonan la perspectiva paradójica (todo el toroide paradójico). Esto revela la esencia y el origen de todo el razonamiento lógico: una conveniencia social extraída de un contexto paradójico. La extracción, sin embargo, reduce a priori las posibilidades (las alternativas disponibles) para estos observadores.

Razonamiento lógico

Lógicos y matemáticos han esculpido y extraído (laboriosamente, brillantemente) todo el edificio del razonamiento lógico desde estos mismos bucles paradójicos, de modo que este edificio dé placer al mayor número posible de lógicos y matemáticos. El esculpir y extraer, como antes, reducen a priori las posibilidades (las alternativas disponibles). Lo mismo vale para la ciencia y sus aplicaciones, y para cualquier otra actividad en la cual los observadores intentan sólo el razonamiento lógico.

El razonamiento lógico solo, y un lenguaje “lógico” derivado de él, a pesar de todos los beneficios que ha otorgado a los humanos, más que nada permitiéndoles construir y destruir cosas juntos, los ha privado de sabiduría; y debido a que diferentes grupos de humanos a menudo no comparten el mismo razonamiento lógico, también ha estimulado su irracionalidad, exacerbada por diferencias excesivas e innecesarias de riqueza y poder.

Los observadores que usan sólo el razonamiento lógico siempre han tratado de alejarlo de su origen paradójico, como lo muestran las historias de las lógicas y las matemáticas. Estas historias muestran una abundancia de ramas que nacen de estas disciplinas y dedicadas, la mayoría , si no todas, a erradicar o aislar las paradojas. Esto revela disciplinas concentradas en ellas mismas dentro de sus propios lenguajes y su creciente abstracción; desprovistas además de una visión filosófica, las hace cada vez más inadecuadas para contribuir a una mejor sociedad de humanos.

Un ejemplo

Muchos bucles paradójicos han inspirado aplicaciones útiles o inútiles tales como el inversor lógico con realimentación usado como un oscilador (e.g., en el corazón de las computadoras digitales), o el oscilador electromagnético usado en los timbres eléctricos, o la paradoja del mentiroso que inspiró y mortificó a muchos lógicos y matemáticos. El ejemplo presentado más abajo sugiere además la perspicacia que las paradojas pueden otorgar a las lógicas, a las matemáticas y a las ciencias, siempre que se les permita formar parte del razonamiento; como si los humanos prestaran oído a los alborotadores en lugar de hacerlos callar.

Cuando un observador entra de noche a una pieza, el observador suele encender una luz eléctrica usando un interruptor cerca de la puerta. El circuito eléctrico correspondiente puede verse en la figura siguiente. V representa una fuente de voltaje y L representa la luz. El interruptor INT permite el flujo de corriente (luz encendida) cuando está cerrado y lo impide (luz apagada) cuando está abierto.

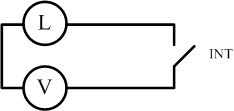
Si la pieza tiene varias puertas, el observador desearía tener un interruptor cerca de cada puerta, de modo que la misma luz pueda encenderse y apagarse desde cada uno de los interruptores.

Un enfoque paradójico de este problema ofrece una solución interesante, llena de posibilidades y significados. Modifique el circuito como sigue:

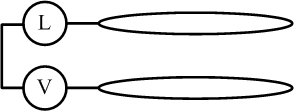
En lugar del interruptor el circuito tiene ahora dos anillos de alambre eléctrico. Imagine estos anillos como los dos bordes de la cinta de papel considerada más arriba. Si el observador logra girar esta cinta para formar una cinta de Möbius, los dos anillos formarán un alambre continuo que cerrará el circuito y encenderá la luz. El observador puede hacer esto con un interruptor Doble Polo Doble Tiro (DPDT) como sigue:

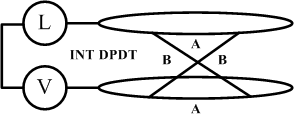
Con el interruptor en la posición A (A cerrado, B abierto), los dos anillos de alambre permanecen aislados uno del otro (luz apagada). Con el interruptor en la posición B (A abierto, B cerrado), los dos alambres se cruzan (giran) cada uno hacia el otro formando un alambre continuo y encendiendo la luz. El observador puede conectar tantos de estos interruptores como desee alrededor de los anillos. Tal como en el bucle paradójico de proposiciones, sólo un número impar de interruptores en la posición B (giro) encenderá la luz. Nótese que la operación (utilidad) del circuito contempla lógica y paradoja, distinción y no distinción. Si el observador coloca un interruptor cerca de cada puerta y los conecta de esta manera, el observador podrá encender y apagar la luz desde cada una de esas puertas.

Además, dependiendo de dónde, entre los interruptores, el observador conecta la fuente de voltaje y la luz a los anillos de alambre, resultan distintas operaciones de los interruptores.

(Construí este circuito con cinco DPDT interruptores y opera tal como lo he descrito).

Una metáfora

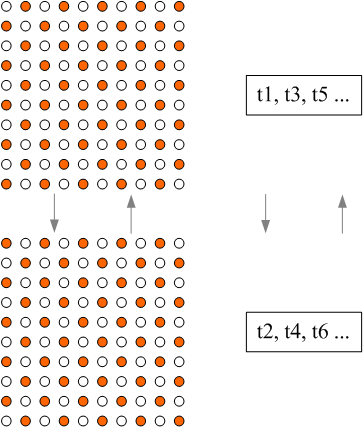
Imagine una red, por ejemplo, de cien nodos dispuestos en una matriz 2-D (bidimensional) de 10x10 elementos interconectados horizontal y verticalmente (una interconexión 2-D de nodos). Haga de cada nodo un oscilador y su oscilación observable como una luz que el nodo enciende (roja) y apaga (blanca) con una cierta frecuencia. (Vea la primera mitad de la figura siguiente). Un oscilador básico consiste de un inversor lógico dentro de un bucle paradójico (un bucle con un giro como una cinta de Möbius). Tal como una paradoja la oscilación sucede en un tiempo y un espacio que resulta del observador contemplando el oscilador desde una perspectiva lógica. (Muchas configuraciones de elementos en un bucle recurrente pueden hacer osciladores de distintos tipos tal como eléctricos, mecánicos, ópticos, biológicos, etc.). En la red, todos los osciladores oscilan aproximadamente a la misma frecuencia. Cuando un nodo apaga su luz, envía una señal excitadora a sus cuatro vecinos (arriba, abajo, derecha e izquierda, incluyendo un retorno a través de los bordes de la matriz) los cuales encienden sus luces. Esta actividad proveniente de los nodos sincroniza la red entera de modo que ella oscila encendiendo y apagando luces alternadamente (vertical y horizontalmente) en los instantes (t1, t2, t3, t4, t5, t6…) y además provee innumerables bucles paradojales. El retorno a través de los bordes, estructural o no, opera desde una fila (columna) par a una impar o desde una impar a una par. (Construí esta red y opera tal como la describe el texto).

La estabilidad dinámica de la actividad en la red, claramente más compleja que aquélla en cada uno de sus nodos, ofrece muchos contextos paradójicos (todas las posibilidades) donde el observador puede elegir (distinguir) entre alternativas concurrentes:

• Observando la actividad de la red (luces que se encienden, otras que se apagan), el observador puede concentrar su atención en una luz que acaba de encenderse, y luego cuando se apaga elegir una de sus cuatro luces vecinas (cuatro posibilidades) que ahora se han encendido. Entonces, concentrar su atención en la luz elegida y cuando ésta se apague, elegir una de sus cuatro luces vecinas que acaban de encenderse, y así hasta el infinito, formando una trayectoria dibujada por las luces visitadas. En cada luz visitada por el observador, las cuatro luces vecinas, como un contexto paradójico, alternan lógicamente arriba, abajo, derecha o izquierda y fusionan paradójicamente arriba, abajo, derecha e izquierda. (Vea la última figura de los toroides lógicos y paradójicos).
  
  
• El observador también puede elegir seguir el movimiento de una o más diagonales de luces encendidas. Mientras la red oscila, el movimiento lleva a estas diagonales hacia la esquina (arriba, izquierda) de la matriz y hacia la esquina (abajo, derecha). El observador también puede elegir diagonales cuyo movimiento las lleva hacia la esquina (arriba, derecha) y hacia la esquina (abajo, izquierda). Para el observador las diagonales, como un contexto paradójico, alternan lógicamente, hacia arriba o hacia abajo, y fusionan paradójicamente hacia arriba y hacia abajo.
  
  
• Lo mismo vale para las diagonales hechas de luces apagadas, si el observador elige seguir estas diagonales en lugar de las otras.
  
  
• El observador también puede elegir cualquier grupo de luces (digamos 2, 3, 4 … n luces encendidas) y, eligiendo los movimientos de cada luz elegida, formar figuras que resultan de las trayectorias determinadas por todas las elecciones. Por ejemplo, en la mitad inferior de la figura siguiente, un observador ha elegido un grupo de dos luces encendidas (rojas) en una diagonal. Luego, el observador elige, para cada luz, un movimiento vertical (u horizontal) pero en direcciones opuestas y así una y otra vez, como lo muestran las flechas. Mientras la red oscila este par de luces oscila, para el observador, como un balancín y gira como un molino de viento si los movimientos verticales y horizontales alternan.

(Si el número de luces elegidas para cada grupo crece, el número de figuras posibles formadas a medida que el observador elige las luces vecinas aumenta aún más. Esto sucede aún para una red de modesto tamaño como la considerada aquí. Nótese que el observador no puede seguir todas las figuras posibles, de modo que pierde inevitablemente aquellas que no sigue, tal como cualquier observador sólo puede manejar hasta cierto punto su ambiente, perdiendo el resto).

• Y muchas otras.
  

Vea la figura animada.

Vea la figura animada.

Las elecciones del observador no afectan la oscilación de la red pero sin la actividad de la red el observador no puede elegir. Por otro lado, sin un observador la actividad de la red no tiene sentido.

Agregando sensores de luz a la red, una luz externa (a la red) puede afectar la estabilidad dinámica de la actividad en la red y algunas luces vecinas no se encenderán como previsto o viceversa, variando el número de elecciones posibles para el observador. Esto sugiere que la red puede tener cualquier forma: regular, como hemos visto, o irregular.

Como la red genera luz algunas luces pueden actuar como efectores y la red puede interactuar con otra red o con ella misma (e.g., usando un espejo).

Para un observador, algunas luces pueden representar superficies efectoras y algunos sensores de luz pueden representar superficies sensorias de la red. En una red como ésta, cualquier actividad en alguna parte de la red conduce a actividad en alguna otra parte de la red, incluyendo el “ambiente exterior” a la red.

Inhibiendo la actividad de algunas luces, un estímulo externo (e.g., luz) puede conducir al aislamiento parcial o total de otras luces. Estas continuarán oscilando por sí mismas, pero la actividad de la red se desintegrará y dejará de oscilar como una entidad.

Observemos ahora a la red de luces oscilantes como una sociedad de organismos individuales (las luces o grupos de ellas) que interactúan con sus vecinos inmediatos. Bajo ciertas circunstancias estas interacciones pueden corresponder a aquéllas de una sociedad viable, por ejemplo, un hormiguero, una colmena, un grupo humano. Notemos que para un observador no afectado por el funcionamiento de estas “sociedades”, éstas no hacen sentido excepto como redes oscilantes que sólo oscilan (no importa cuán compleja la oscilación) como la matriz de luces ya descrita.

Imaginemos a un visitante en una tierra extranjera donde los habitantes hablan una lengua que el visitante no entiende, y donde los habitantes no entienden el lenguaje del visitante. Durante un tiempo el visitante no interactúa con los habitantes y por lo tanto el visitante actúa sólo como un observador de ellos y viceversa mientras ninguno de los dos perciba al otro como un peligro o un estorbo. Las sociedades o grupos que el visitante encuentre aparecerán sólo como redes que sólo oscilan hasta que el visitante aprenda el lenguaje y participe en la oscilación (la danza).

La actividad de estas redes oscilantes puede resistir algún daño local (algunos nodos dejan de oscilar, algunas señales excitadoras o inhibidoras bloqueadas, etc.) pero la red como un todo continúa su danza, fusionando estabilidad e inestabilidad dinámicas y enriqueciendo así la vida del grupo o sociedad y la de sus miembros. Con un daño mayor la actividad de la red puede extinguirse.

Notemos que la actividad (oscilación) en la red como un todo se mantiene a sí misma debido a que cualquier actividad en algún lugar de la red conduce a nueva actividad (integrada, sincronizada) en otro lugar, actividad que retorna a través de muchos bucles paradójicos posibles a la actividad del primer lugar. (Un círculo, una esfera, con su centro en todas partes y con su circunferencia, superficie, en ninguna parte).

Debería fluir de lo ya dicho que la interconexión 2-D de nodos puede extenderse a una interconexión multidimensional de nodos y que la actividad de los nodos puede hacerse mucho más compleja que la de encender o apagar una luz y que las señales entre los nodos también pueden crecer en complejidad. Los organismos vivos, por ejemplo, interactúan usando una variedad de portadores de señales simples y complejas: electro-químicos, químicos, luz, sonido, danza, etc., y, por supuesto, el lenguaje humano.

La figura que sigue representa los instantes (t1, t2, t3, t4, t5, t6 …) de un nodo (al centro), sus vecinos y los vecinos de sus vecinos en una interconexión multidimensional de nodos. Como antes, cuando un nodo apaga su luz (blanca) todos sus vecinos encienden sus luces (rojas). Con n = 4 la figura representa una interconexión 4-D (D1, D2, D3, Dn) de nodos con 8 posibilidades claramente dibujadas en cada nodo. (Si Dn representa el tiempo la figura puede representar un espacio-tiempo de 4-D). (Construí esta red y opera tal como la describe el texto).

Vea la figura animada.

(Una interconexión 1-D (unidimensional) de nodos ofrece al observador un contexto paradójico con 2 posibilidades en cada nodo (2 vecinos); una interconexión 2-D de nodos, como la que hemos considerado antes, ofrece en cada nodo 4 posibilidades (4 vecinos); una 3-D ofrece 6; una 4-D ofrece 8; y una n-D ofrece 2n posibilidades. (Una 0-D no ofrece ninguna).)

Para contemplar más de cuatro dimensiones el lector debe imaginar o dibujar los nodos adicionales y sus interconexiones al nodo central, entre D3 y Dn, y entre –D3 y –Dn, como lo sugiere la figura.

A pesar de este aumento en complejidad, una red no impedida de elementos individuales todavía oscila sin importar cuán complejos los nodos, sus señales, o su comportamiento observado, y sin importar cuantas dimensiones involucren sus interacciones.

Las propiedades esenciales de la red 2-D no han cambiado: puede tomar cualquier forma, su actividad no tiene bordes, cualquier actividad conduce a más actividad integrada, resiste daño local y temporal, puede interactuar con otras redes similares, y un daño mayor o permanente puede desintegrar la actividad de la red como una entidad oscilante.

Si las hormigas pierden su “lenguaje” (señales entre nodos) la actividad del hormiguero se desintegra como una entidad. Lo mismo les acontece a las abejas y a su colmena. Y así le acontecerá a todos los organismos sociales (incluidos los humanos) y sus sociedades, si pierden su “lenguaje”.

Nótese, sin embargo, que para un conjunto de nodos complejos tal como los humanos en sociedad, un “lenguaje” preciso y/o limitado como el de las hormigas o abejas, ya significa una pérdida. Un individuo complejo, ya una entidad en sí mismo y no totalmente sometido a una sociedad (tal como una hormiga en un hormiguero, una abeja en una colmena, etc.), requiere una comunidad de individuos complejos que interactúen con la riqueza y flexibilidad necesarias para lograr y preservar las mejores condiciones de vida para cada individuo en la comunidad.

Desgraciadamente la mayoría de las sociedades humanas se organizan como jerarquías rígidas que requieren miembros predecibles (triviales), los cuales perderán rápidamente la riqueza y flexibilidad de sus interacciones reduciéndolas a un parloteo trivial, no diferente del “lenguaje” de las hormigas o abejas. Puede desarrollarse una sociedad, pero no de humanos.

Las jerarquías reemplazan el pensar y la conversación con rituales, seculares o religiosos, los cuales no llevan al pensar ni a la conversación. Esto revela sociedades intranquilas respecto al presente, melancólicas respecto a un pasado primitivo y con presentimientos de un futuro sin humanos.

Relajando las distinciones arbitrarias necesarias para establecer y mantener sociedades jerárquicas, hasta el punto de eliminar las jerarquías, permitirá consecuentemente recobrar la riqueza y flexibilidad de las interacciones y que el pensar y la conversación florezcan otra vez.

Consideremos la red de osciladores como una comunidad de observadores dotada de una actividad no jerárquica. Consideremos las perturbaciones que afectan a esta actividad sin desintegrarla, pero que pueden constituir estímulos para conflictos imprevisibles. La flexibilidad de la actividad no jerárquica le permite incorporar conflictos permanentes en una nueva danza (oscilación) o resistir conflictos pasajeros y recuperar su oscilación original.

Además, una comunidad con actividad no jerárquica no requiere distinciones rígidas y, por lo tanto, puede superar conflictos que no tienen solución dentro de las jerarquías.

Razonamiento paradójico

Un observador que razona lógicamente no recibe bien las paradojas. Este observador, que rechaza a priori el máximo de posibilidades, considera las paradojas como razonamientos erróneos. Por lo tanto, un observador razonando lógicamente considera “razonamiento lógico” o “razonamiento paradójico”.

Para un observador que razona paradójicamente todas las posibilidades cuentan, fusionándose entre ellas. En consecuencia, para un observador que razona paradójicamente, razonar “lógicamente” o “paradójicamente” se fusionan en razonar “lógica y paradójicamente”.

Un organismo vivo se produce y se mantiene a sí mismo como una red cerrada y paradójica de procesos y componentes que se distingue como un observador de un ambiente que resulta de la misma distinción.

Un organismo vivo, tal como una célula o un organismo multicelular, necesita un ambiente favorable para sobrevivir. También puede jugar el papel de un procesador que, interactuando con otros organismos vivos similares, puede formar parte de una cadena cerrada de procesadores, los cuales, dado o haciendo un ambiente favorable, puede conducir a un nuevo organismo vivo hecho de organismos vivos. Para sobrevivir, este nuevo organismo debe proveer un ambiente favorable para la supervivencia de los organismos constituyentes y para su reemplazo a través de la reproducción o de otra forma. Este nuevo estado de cosas requiere que los organismos constituyentes abandonen su forma imprevisible (su razonamiento paradójico) a favor de una forma previsible (un razonamiento lógico) exigido por el nuevo organismo.

Esto le sucede, por ejemplo, a las hormigas y a las abejas al someterse al hormiguero y a la colmena, respectivamente, el nuevo organismo vivo.

Retornando brevemente a la red de osciladores como una metáfora, cada nodo aislado oscila libremente, impulsado por su bucle paradójico interno. Como parte de la red, sin embargo, debido a las señales de otros nodos, debe mantener su oscilación sincronizada, tal como lo exige la lógica de la red.

La actividad de un sistema nervioso, así como la de otras redes, requiere la presencia de osciladores interconectados (una o más neuronas dentro de uno o más bucles paradójicos) que generan y mantienen esta actividad. Así, las neuronas forman una red de osciladores llamada el sistema nervioso. De otra manera, la actividad del sistema nervioso desaparecería y junto con ella las muchas posibilidades que ofrece a los organismos vivos.

La estructura tridimensional del sistema nervioso contiene innumerables neuronas con innumerables interconexiones. Como cada neurona conecta con muchas otras neuronas, el sistema nervioso, a pesar de su estructura tridimensional, funciona en forma multidimensional independiente de la posición de las neuronas y de las restricciones del espacio 3-D. Esto le otorga el enorme potencial para activar gran cantidad de canales, incluyendo aquellos que involucran el medio ambiente a través de efectores y sensores, esencialmente todas las posibilidades, como en un contexto paradójico, donde un observador hace las distinciones tentativas necesarias para interactuar consigo mismo y con su medio ambiente. Los sensores y efectores proveen la primera distinción tentativa: el observador distinguido de su medio ambiente, habitado por el mismo y por otros observadores.

Un observador, con un sistema nervioso potencialmente tan complejo como el de un infante humano, emerge a un mundo ya poblado y formado por otros observadores humanos.

Los sistemas nerviosos de los niños se desarrollan a través de interacciones con sus alrededores y con ellos mismos considerando todas las posibilidades, incluyendo las emociones, los sentimientos y a otros observadores, haciendo uso exhaustivo de sus efectores y sensores.

La actividad del sistema nervioso de los niños ofrece un contexto paradójico (todas las posibilidades) dentro del cual se desarrolla su razonamiento paradójico y lógico.

Otros observadores, algunos indiferentes, algunos bien intencionados, guiarán a los niños en su exploración del mundo; algunos estimularán su razonamiento lógico con una visión restringida; otros estimularán su razonamiento paradójico con todas sus posibilidades; muchos intentarán instruirlos en cómo ellos ven el mundo. Todos influirán en los niños, en mayor o menor grado.

Un niño afortunado mantendrá vivo su razonamiento paradójico y así contemplará todas las posibilidades en un contexto paradójico dentro del cual, mediante un pensamiento independiente, hará las distinciones tentativas que necesite. Esto llevará a un sistema nervioso que mantendrá su curiosidad original, ánimo de conocer y la habilidad de ejercer un pensamiento independiente durante toda la vida de este observador humano. Este observador no dará por sentada la sociedad humana y contribuirá sabiamente a mejorarla sin ideas preconcebidas, prejuicios o dogmas que solamente pueden provenir de sólo razonar lógicamente.

Un niño menos afortunado inhibirá su razonamiento paradójico a favor de un razonamiento lógico, desarrollando así un sistema nervioso que perderá su curiosidad original, su ánimo de conocer y su pensamiento independiente. En el mejor de los casos este niño crecerá como un miembro indiferente de la sociedad humana, alguien que preferirá instruir que educar a los jóvenes. Una sociedad desafortunada con la mayoría de sus miembros inmersos en un razonamiento lógico sucumbirá a la recurrencia ya mencionada en el prefacio.

Poco después de su temprana infancia los humanos también desarrollan la capacidad de reflexionar sobre sus acciones y pensamientos. Una sociedad desafortunada inhibe este desarrollo a través de jerarquías arbitrarias que limitan las posibilidades del sistema nervioso y pronto la mayoría de sus miembros pierden esta capacidad y viven totalmente ignorantes de este vacío dentro de otros y dentro de ellos mismos.

En lugar de confiar en el razonamiento lógico y en la búsqueda de una “verdad”, el Tractatus propone confiar en el razonamiento paradójico y en explorar todas las posibilidades; el razonamiento lógico aparece así bajo una nueva luz.

Así como con las paradojas, ningún observador puede “explicar” el Tractatus o ninguna de sus proposiciones sin trivialización y pérdida. Las proposiciones del Tractatus no dicen, no enseñan ni explican; muestran. Ellas invitan al observador a eludir las comodidades del trivializar, a explorar y a aumentar, a través de la educación, las alternativas, a fusionar paradojas y lógicas, y a evitar las distinciones instruidas. Aceptar esta invitación requiere coraje porque el Tractatus destruye muchas nociones y hábitos enraizados, alejándose de la “civilización” , de las formas de vida y del lenguaje contemporáneos.