EINFÜHRUNG

Ordnung und* Chaos: stimuliert Phantasie und Kreativität.
Ordnung or** Chaos: blockiert Phantasie und Kreativität, erlauben einigen grenzenlose Macht zu entwickeln, um in das Leben anderer einzugreifen.

* und: das eine durchdringt das andere.
** oder: das eine schließt das andere aus.

Dieser Tractatus bietet ein neues, oder lange vergessenes Sprachspiel an. Er tut dies nicht mittels Definitionen oder Erklärungen sondern durch Zeigen, so als würden Ideen ausgesprochen und gleichzeitig auf sie gezeigt. Er lädt Beobachter dazu ein, hauptsächlich durch Metaphern, neue Arten des Sehens (Verstehens) zu erkunden sowie neue Arten Wünsche und Interaktionen auszudrücken.

Die Beschreibung sämtlicher Phänomene als Prozesse oder Netzwerke mag uns mit Leichtigkeit einleuchten. (Vergegenwärtigen Sie sich etwa Phänomene wie die Bewegung eines Körperteils, die Explosion eines Sterns, die „Kollisionen” von subatomaren „Partikeln”, den „Anfang” des „Universums” sowie dessen anschließende Transformationen etc.).

Dass ein geschlossenes Netzwerk von Prozessen sich selbst als Beobachter einer Umwelt identifizieren kann, welche durch eben diese Unterscheidung selbst hervorgebracht wurde, mag uns weniger leicht verständlich erscheinen. Vergegenwärtigen Sie sich weiterhin: (1) dass die unterschiedene Umwelt den Beobachter (das geschlossene Netzwerk von Prozessen) beinhaltet und (2) dass aus Sicht des Beobachters diese und weitere Unterscheidungen, die aus der Interaktion des Beobachters und der Umwelt hervorgehen, sowohl logisch und paradox erscheinen. In anderen Worten (paradoxerweise) durchdringen sich für den Beobachter alle Möglichkeiten gegenseitig (zum Beispiel existieren und nicht existieren, drinnen und draußen, rot und blau und grün und... etc.) und (logischerweise) unterscheiden sich die Möglichkeiten für den Beobachter voneinander (existieren oder nicht existieren, drinnen oder draußen, rot oder blau oder grün oder... etc.).

Lebende Organismen, mit oder ohne Nervensystem, stellen Beispiele geschlossener Netzwerke von Prozessen dar. Ein Nervensystem, selbst ein Netzwerk geschlossener Prozesse, interagiert mit seiner Umwelt durch geschlossene Netzwerke von Prozessen, die sowohl seine sensorischen Oberflächen als auch seine effektorischen Oberflächen involvieren. Das Nervensystem interagiert daher mit seiner Umwelt (paradoxerweise) in und außerhalb seiner selbst und (logischerweise) in oder außerhalb seiner selbst.

Weitgehend durch ihre Biologie bestimmt, unterscheiden ein oder mehrere Beobachter, logisch denkend, eine Welt „dort draußen”, die aus Objekten und Ereignissen besteht. Mit diesen Objekten und Ereignissen assoziieren sie (durch weitere Unterscheidungen) spezifische Möglichkeiten, als Resultat wahrnehmerischer und anderer Einschränkungen sowie von Versuchen sozial zu interagieren. Doch diese Versuche beinhalten Schritte hin zu Trivialität und weg vom Denken in Paradoxen. Soziales Wissen, sei es „objektiv” oder „subjektiv”, so wie es von Logikern, Mathematikern, Naturwissenschaftlern, Technologen und anderen betrieben wird, ist keine Ausnahme. Ein Beobachter mag solche Versuche nichtsdestotrotz solange wertschätzen wie sie zu Konversation führen und somit Trivialisierung (Instruktion) des einen durch den anderen oder der Mehrheit durch eine Minderheit vermeiden.

Zwei oder mehrere individuelle Beobachter können eine gemeinsame Welt „dort draußen” nicht unterscheiden, es sei denn dass geeignete Anzeichen sie davon überzeugen. Von solchen Anzeichen ausgehend können menschliche Beobachter durch logisches Denken Schlussfolgerungen über die Welt „dort draußen” ziehen, die nicht standhalten werden bis andere Anzeichen sie untermauern und somit die ursprüngliche Unterscheidung einer Welt „dort draußen” bestätigen. Da neue Anzeichen alten widersprechen können, findet dieser Prozess (Anzeichen, Schlussfolgerungen, neue Anzeichen, neue Schlussfolgerungen) kein Ende. Er kann sogar die ursprüngliche Unterscheidung einer Welt „dort draußen” in Frage stellen, was wiederum logisches Denken selbst in Frage stellen und stattdessen paradoxes Denken nahelegen kann.

Kein Beobachter „löst” oder „erklärt” Paradoxe ohne dabei Verluste hinnehmen zu müssen. Diese Sicht scheint, wie im Tractatus gezeigt wird, denjenigen Gesellschaften essenziell zugrunde zu liegen, die Menschen durch Bildung und Kunst und Philosophie entwickeln sollten. Der Tractatus sagt nicht, lehrt nicht und erklärt nicht was zu lehren sei, doch er zeigt Bildung so als deute er dabei mit dem Finger darauf. Er zeichnet auch die Ursprünge dieser anscheinend empörenden Aussagen nach bis hin zur Quelle aller Propositionen: die paradoxe Essenz des Beobachters.

Wenn Menschen nicht ihren selbstgemachten Unzulänglichkeiten zum Opfer fallen, dann sollten die Folgen ihnen helfen sich selbst und die Konsequenzen ausschließlich logischen Denkens, wie es von Logikern, Mathematikern, Naturwissenschaftlern, Technologen und anderen betrieben wird zu erkennen (verstehen). Auf der Suche nach Wahrheit, als suchten sie nach einem Gott, übersetzen sie alles in ihre eigene Sprache und verfehlen dabei aufs Gründlichste den Sinn. Diejenigen, die die genannten Disziplinen praktizieren vergessen oder bekämpfen schnell ihren paradoxen Ursprung, hauptsächlich weil sie sich für „besser gestellt” und/oder „zufrieden” halten. Diejenigen, die glauben werden schnell diesen Status erreichen und logisches Denken befürworten, einfordern oder sich ihn anpassen, ohne Widerspruch oder Paradoxe, und somit einen status quo erzwingen.

Von Logik zu Paradoxen

Vergegenwärtigen Sie sich eine Aneinanderreihung von Wörtern (einen Satz) und nennen Sie sie eine Proposition (eine Aussage), die von einem oder mehreren Beobachtern erfunden wurde, um etwas in einem gegebenem Kontext festzustellen.

Propositionen können für unterschiedliche Gruppen, bestehend aus einem oder mehreren Beobachtern, unterschiedliche Bedeutungen haben.

Eine Gruppe von Beobachtern kann durch paradoxes Denken vorläufige gemeinsame Bedeutungen für Propositionen durch die Sprachspiele finden, die ihre Formen ihres Lebens bestimmen.

Eine Gruppe von Beobachtern kann durch logisches Denken herausfinden, dass einige Propositionen nicht auf sich selbst referieren und dass ein Beobachter oder eine Gruppe von Beobachtern diesen Propositionen logische Werte (z.B. in einer zweiwertigen Logik: wahr, falsch) zuweisen und festlegen muss. Andere Beobachter mögen damit nicht übereinstimmen und andere Werte mit Argumenten verteidigen.

Andere Propositionen referieren auf sich selbst (selbstreferenzielle Propositionen) und bestimmen somit ihre eigenen logischen Werte, z.B., L: „Proposition L hat jetzt und hier den Wert wahr”. Ein oder mehrere Beobachter können wählen und L entweder einen logischen Wert (wahr, falsch) zuweisen, und da L sich auf sich selbst bezieht, gestattet es keine Argumente die diese Wahl bestätigen oder in Frage stellen.

Einige selbstreferenzielle Propositionen, wie etwa die Proposition „P: Proposition P hat jetzt und hier den Wert falsch”, bestimmen ihren eigenen „logischen Wert” als „wahr und falsch” und verhindern somit dass sich der Beobachter für wahr oder falsch entscheidet. Wenn ein oder mehrere Beobachter, logisch denkend, annehmen, diese Proposition habe jetzt den Wert wahr, dann müssen sie, dieser Annahme folgend, bald akzeptieren, dass ihr Wert falsch ist. Wenn sie annehmen der Wert der Proposition sei falsch, dann müssen sie ihn bald als wahr akzeptieren und so weiter. Für diese Beobachter oszillieren die Werte: wahr, falsch, wahr, falsch... wenn sie versuchen einen Wert zu bestimmen. Nennen Sie diese Proposition ein Paradox.

Unglücklicherweise vergessen viele Autoren, die über Paradoxe schreiben Selbstreferenz und das gegenseitige Durchdringen unterschiedlicher Möglichkeiten als essenzielle Aspekte von Paradoxen. Dies hat die bedauerliche Folge, dass viele Rätsel, Puzzles und Knobelspiele etc... für Paradoxe gehalten werden.

Das Paradox erlaubt dem Beobachter nicht, der Proposition einen Wert „wahr” oder „falsch” zuzuweisen, es sei denn als Teil einer Oszillation, wodurch der Beobachter eingeladen wird, paradoxes Denken in Betracht zu ziehen und beide Werte einander durchdringen zu lassen (sämtliche Möglichkeiten in diesem Fall) zu „wahr und falsch”.

Logisch denkend kann der Beobachter lediglich beide Werte in einer Zeit oder in einem Raum abwechselnd in Betracht ziehen in Folge des Versuchs des Beobachters das Paradox von einer logischen Perspektive aus zu betrachten.

Paradox denkend, lässt der Beobachter „wahr” oder „falsch” einander durchdringen zu „wahr” und „falsch”, was zu einer paradoxen Perspektive ohne Zeit, Raum und ohne Oszillation führt.

Mit paradoxem Denken lässt der Beobachter jedoch ohne Konflikt alle Möglichkeiten einander durchdringen. Daher lässt der Beobachter mit paradoxem Denken auch paradoxes oder logisches Denken einander zu paradoxem und logischem Denken durchdringen. Somit kann der Beobachter, paradox denkend, auch provisorische Unterscheidungen in Raum und Zeit fällen.

In einer selbstreferenziellen Schleife von Propositionen wie der folgenden, abgeleitet von der oben genannten L, werden alle Propositionen, in Abhängigkeit von dem was der Beobachter für eine der Propositionen, z.B. L1, wählt, entweder den Wert „wahr” oder den Wert „falsch” haben (und keine Oszillation entsteht):

			t1	t2 ...
L1: „L2 hat jetzt und hier den Wert wahr.”			W(F)	W(F)…
L2: „L3 hat jetzt und hier den Wert wahr.”			W(F)	W(F)…
Ln: „L1 hat jetzt und hier den Wert wahr.”			W(F)	W(F)

Eine selbstreferenzielle Schleife wie die folgende, abgeleitet von der oben genannten Proposition P, wird dem Beobachter nicht erlauben, ihren enthaltenen Propositionen Werte zuzuweisen, da ihre Werte logisch oszillieren und sich für den Beobachter wie zuvor einander paradox durchdringen werden (beachten Sie dass nun, da der Beobachter logisch denkend den Wert jeder Proposition zuweist, die Werte die Schleife aus Propositionen durchlaufen und somit die Oszillation von Werten etwas komplexer gestaltet als hier gezeigt):

			t1	t2	t3 ...
P1: „P2 hat jetzt und hier den Wert wahr.”			W	F	W ...
P2: „P3 hat jetzt und hier den Wert wahr.”			W	F	W ...
					...
Pn: „P1 hat jetzt und hier den Wert falsch.”			W	F	W ...

So wie Proposition P legt diese Schleife von Propositionen dem Beobachter paradoxes Denken nahe.

Wenn ein Beobachter einen schmalen Streifen Papier nimmt und dessen Enden aneinander klebt, dann formt er einen Ring mit zwei Seiten (innen und außen) und zwei Kanten (rechts und links oder oben und unten, je nach dem wie der Beobachter den Ring hält). Nimmt er an, dass je eine der Seiten (oder Kanten) des Rings mit einem Wert (W, F) korrespondiert, kann der Beobachter den ganzen Ring als Metapher sehen für die Schleife aus Propositionen, die von L abgeleitet wurde.

Wenn der Beobachter ein Ende des Papierstreifens um 180 Grad verdreht bevor er es an das andere Ende klebt, so formt er ein Möbius-Band mit einer Seite und einer Kante (siehe Ring und Möbius-Band im folgenden Abschnitt). Dieses Band entspricht der paradoxen, von P abgeleiteten Schleife aus Propositionen, in der sich, aus Sicht des Beobachters der die Schleife durchläuft, logische Werte abwechseln (in einer Zeit und einem Raum) und zwei paradoxe Werte sich in einen durchdringen (keine Zeit, kein Raum). Ebenso wechselt das Band für den Beobachter der entlang des Bandes läuft, logisch zwischen zwei Seiten (in einem Raum und einer Zeit) und beide Seiten durchdringen einander paradox in eine einzige (keine Zeit, kein Raum). Gleichsam wechseln logisch beide Kanten (in einer Zeit, in einem Raum) und durchdringen einander paradox in eine einzige (keine Zeit, kein Raum). Beachten Sie, dass Proposition n mit der Verdrehung korrespondiert und dass jede ungerade Anzahl von Verdrehungen das Paradox aufrecht erhält, während jede gerade Anzahl von Verdrehungen es zerstört indem sie eine Unterscheidung einführt.

Logische und paradoxe Toroide

Wenn ein Beobachter anstatt eines Bandes eine Röhre mit polygonalem Querschnitt hat, die in sich geschlossen eine toroide Form mit 3, 4, 5... oder n Seiten hat, und wenn jede Seite eine Möglichkeit repräsentiert (z.B. einen logischen Wert in einer Logik mit multiplen Werten oder eine Komponente in einem geschlossenen Netzwerk aus Prozessen und Komponenten), so hat der Beobachter eine logische toroide Form aus der er mit einer geeigneten Verdrehung (360/3 Grad = 120 Grad bei 3 Seiten, 360/4 Grad = 90 Grad bei 4 Seiten, 360/n Grad bei n Seiten (n Möglichkeiten)) einen paradoxen Toroid (eine Seite, eine Kante) formen kann.

Ring und Möbius-Band: (2 Seiten <=> 1 Seite, 2 Kanten <=> 1 Kante)

Logische and paradoxe Toroide: (3 Seiten <=> 1 Seite; 3 Kanten <=> 1 Kante)

Logische and paradoxe Toroide: (4 Seiten <=> 1 Seite; 4 Kanten <=> 1 Kante)

Aus Sicht des Beobachters, der die entstandene Seite der Länge nach verfolgt, wechselt der paradoxe Toroid zwischen n Seiten in einem Raum und in einer Zeit und gleichzeitig durchdringen sich die n Seiten paradox zu einer einzigen Seite, wodurch Raum und Zeit eliminiert werden. Jedes Mal wenn der logisch denkende Beobachter nach einer Umrundung des paradoxen Toroids wieder am Ausgangspunkt ankommt, wird der Beobachter auf einer anderen (und, paradox, derselben) Seite stehen. Der paradoxe Toroid legt dem Beobachter auch paradoxes Denken nahe.

Vergegenwärtigen Sie sich nun dass ein logischer Toroid als Metapher für eine Menge von Komponenten (die Seiten des Toroids), die sich nicht verändern (kein Prozess, keine Aktivität), die statischen Möglichkeiten nicht-lebendiger Dinge repräsentieren können.

Als eine Metapher für eine Menge sich (durch Prozess) ineinander verändernder Komponenten repräsentiert ein paradoxer Toroid jedoch die dynamische Stabilität, die im Herzen aller lebenden Organismen und im Herzen des Nervensystems liegt.

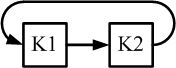
Logisch denkend sehen geschlossene Netzwerke sich verändernder Komponenten folgendermaßen aus (für 2 und 3 Komponenten):

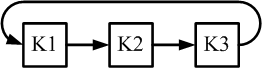Die Pfeile repräsentieren die Prozesse und die Zeiten und Räume, die aus der gewählten logischen Perspektive resultieren.

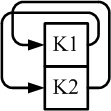
Paradox denkend sehen dieselben Netzwerke aus wie folgt:

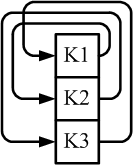Die Pfeile repräsentieren nun Komponenten, die einander durchdringen, Selbstreferenz und Verdrehung (die am besten durch den korrespondierenden Toroid verdeutlicht wird). Weder Zeit noch Raum resultieren von dieser Perspektive.

Von Paradoxen zu Logik

Solange wir es nicht besser wissen macht es Sinn anzunehmen dass menschliche Kinder und ihre Nervensysteme, wenn sie auf die Welt kommen und Teil einer Gesellschaft werden, ihre Umgebungen, sich selbst und ihre Emotionen und Empfindungen beobachten (explorieren), ohne dabei von den Zwängen eines logischen Bezugsrahmens eingeschränkt zu werden.

Vergegenwärtigen Sie sich, dieser Annahme folgend, Beobachtung (Wahrnehmung) als Resultat einer Aktivität geschlossener Schleifen aus Prozessen die, sensorische und effektorische Oberflächen durchquerend, innerhalb und außerhalb des Nervensystems liegen. Da diese Aktivität sämtliche Möglichkeiten einschließt, müssen diese Schleifen den oben diskutierten paradoxen Schleifen ähneln und die Rolle paradoxer Kontexte spielen, in denen uneingeschränkte kindliche Beobachter, paradox denkend (logisches Denken setzt gerade erst ein), provisorische Unterscheidungen treffen.

Ein bescheidenes Maß an Instruktion und Training kann diese Beobachter dazu zwingen, nur einen Teil ihrer paradoxen Toroide (ein Teil den jeder Beobachter mit Teilen der Toroide anderer Beobachter in Übereinstimmung bringen kann) in Betracht zu ziehen, so dass ausschließlich logisches Denken entstehen kann. Weitreichende strenge Instruktion und Training hingegen können den Beobachter zwingen die Verdrehungen ihrer paradoxen Toroide zurückzudrehen (um logische Toride daraus zu machen). Anders als im ersten Fall, der sich als revidierbar herausstellen kann und zu einen halbwegs flexiblen Beobachter führen kann, kann sich der zweite Fall als nicht revidierbar herausstellen und zu einem rigiden Beobachter führen, der ausschließlich logisches Denken in Betracht zieht.

Die meisten Beobachter erliegen diesen Zwangs-Methoden und geben die paradoxe Sicht (den gesamten paradoxen Toroid) auf. Dies offenbart die Essenz und den Ursprung allen logischen Denkens: eine soziale Bequemlichkeit, extrahiert aus einer paradoxen Umwelt. Dieses Extrahieren reduziert jedoch von vorneherein die Möglichkeiten (die verfügbare Auswahl) für diese Beobachter.

Logisches Denken

Logiker und Mathematiker haben (unter größten Anstrengungen, brillant) den gesamten Apparat der Logik eben diesen paradoxen Schleifen entrissen und abgerungen, auf dass dieser Apparat so viele Logiker und Mathematiker wie möglich entzücke. Dieses Entreißen und Abringen reduziert, wie zuvor besprochen, von vornherein die gegebenen Möglichkeiten (die verfügbare Auswahl). Dasselbe gilt für Wissenschaft und ihre Anwendungen sowie für jede Aktivität, in der die Beobachter versuchen, rein logisch zu denken.

Trotz allem was sie ermöglichen - hauptsächlich das gemeinsame Erbauen und Zerstören von Dingen - berauben rein logisches Denken und davon abgeleitete „logische” Sprache Menschen ihrer Weisheit. Und weil unterschiedliche Gruppen von Menschen oft nicht dasselbe logische Denken teilen, haben rein logisches Denken und davon abgeleitete „logische” Sprache auch menschliche Irrationalität stimuliert, was durch exzessive und unnötige Ungleichverteilungen von Reichtum und Macht verschlimmert wird.

Beobachter, die ausschließlich logisch denken, waren, wie die Geschichte von Logik und Mathematik belegt, immer schon bemüht, das logische Denken von seinem paradoxen Ursprung zu distanzieren. Diese Geschichte zeigt eine Vielzahl von Ablegern dieser Disziplinen von denen sich die meisten, wenn nicht alle, der Ausmerzung oder der Isolation von Paradoxen verschrieben haben. Dies ist ein Beleg dafür, dass den in ihnen konzentrierten Disziplinen, in ihren eigenen Sprachen und deren wachsender Abstraktion, die philosophische Richtung fehlt, was sie zunehmend ungeeignet macht einen Beitrag zu einer besseren menschlichen Gesellschaft zu leisten.

Ein Beispiel

Viele paradoxe Schleifen haben nützliche oder nutzlose Anwendungen inspiriert, wie etwa den logischen Invertierer mit Feedback der als Oszillator benutzt wird (z.B. als Taktgeber im Herzen digitaler Computer), oder der elektromagnetische Summer in elektrischen Türklingeln, oder das Paradox des Lügners und den vielen anderen, die viele Logiker und Mathematiker inspiriert und geplagt haben. Das im Folgenden präsentierte Beispiel legt die Erkenntnisse nahe, die Paradoxe der Logik, der Mathematik und den Naturwissenschaften vermitteln können, wenn Menschen sie als Teil des Denkens zuließen; als würden Menschen Unruhestiftern zuhören anstatt sie zum Schweigen zu bringen.

Wenn ein Beobachter nachts einen Raum betritt, dann wird der Beobachter normalerweise ein elektrisches Licht einschalten indem er einen Schalter nahe der Tür betätigt. Unten folgt ein Diagramm des entsprechenden elektrischen Stromkreises. SQ bedeutet eine Spannungsquelle und L bedeutet ein Licht. Der Schalter SCH ermöglicht des Fluss von elektrischem Strom (Licht an) wenn er geschlossen ist und unterbricht des Strom (Licht aus) wenn er geöffnet ist.

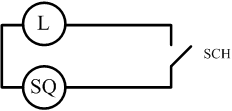
Wenn der Raum mehrere Türen hat, möchte der Beobachter gerne an jeder Tür einen Schalter vorfinden, so dass jeder der Schalter dasselbe Licht ein- oder ausschalten kann.

Ein paradoxer Ansatz liefert eine interessante Lösung für dieses Problem mit vielen Möglichkeiten und Bedeutungen. Modifizieren Sie den Schaltkreis wie folgt:

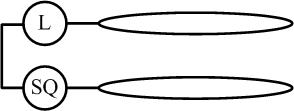
Anstelle des Schalters weist der Schaltkreis nun zwei Ringe aus elektrisch leitendem Draht auf. Stellen Sie sich diese beiden Ringe vor als die beiden Kanten des oben besprochenen Rings aus Papier. Wenn es dem Beobachter gelingt, dieses Band zu verdrehen und so ein Möbius-Band zu formen, so bilden die beiden Ringe eine ununterbrochene Verbindung. Sie schließen somit den Stromkreis und das Licht ist eingeschaltet. Der Beobachter kann dies wie im Folgenden dargestellt mit einem sogenannten Kreuzschalter (oder Polwender) erreichen:

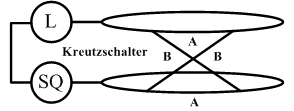
Befindet sich der Schalter in Position A (Verbindungen A geschlossen, Verbindungen B offen), so bleiben die beiden Drahtringe voneinander isoliert (Licht aus). Befindet sich der Schalter in Position B (Verbindungen A offen, Verbindungen B geschlossen), so überkreuzen (verdrehen) sich die beiden Drahtringe miteinander und erlauben einen Stromfluss. Das Licht ist nun eingeschaltet. Der Beobachter kann entlang der beiden Drahtringe so viele dieser Schalter installieren wie er beliebt. Wie in der paradoxen Schleife aus Propositionen schaltet nur eine ungerade Anzahl von Schaltern in Position B (Verdrehung) das Licht ein. Beachten Sie, dass die Arbeitsweise des Schaltkreises Logik und Paradox, Unterscheidung und die Abwesenheit von Unterscheidung beinhaltet. Wenn der Beobachter einen Schalter neben jeder Tür platziert und sie verdrahtet wie hier gezeigt, dann kann er von jeder Tür aus das Licht ein- oder ausschalten.

Darüber hinaus resultieren in Abhängigkeit der Platzierung von Stromquelle und Lichtquelle zwischen den Schaltern entlang der Drahtringe unterschiedliche Operationen aus den Schalterstellungen.

(Ich habe diesen Schaltkreis mit fünf Kreuzschaltern gebaut und er verhält sich wie ich ihn beschrieben habe.)

Eine Metapher

Stellen Sie sich ein Netzwerk aus sagen wir einhundert Knoten in einer 2D (zweidimensionalen) Matrix von 10 mal 10 horizontal und vertikal verbundenen Elementen vor (eine 2D Vernetzung von Knoten). Platzieren Sie an jedem Knoten einen Oszillator und machen Sie die Oszillation jedes Knotens beobachtbar durch eine Lichtquelle, die der Knoten in einer gegebenen Frequenz ein- (rot) und ausschaltet (weiß). (Dies ist in der oberen Hälfte der unten folgenden Grafik dargestellt). Ein einfacher Oszillator besteht aus einem Invertierer in einer paradoxen Schleife (einer Schleife mit einer Verdrehung wie etwa ein Möbius-Band). So wie ein Paradox entwickelt sich die Oszillation in einer Zeit und in einem Raum basierend auf der Ansicht eines Beobachters, der den Oszillator aus einer logischen Perspektive betrachtet. (Viele Konfigurationen von Elementen in einer wiedereintretenden Schleife können unterschiedliche Arten von Oszillatoren von unterschiedlicher Komplexität hervorbringen, wie etwa elektrische, mechanische, optische, biologische etc. Oszillatoren.). In dem Netzwerk oszillieren alle Knoten in etwa mit derselben Frequenz. Schaltet ein Knoten seine Lichtquelle aus, so sendet er ein Stimulations-Signal an seine vier Nachbarn (oben, unten, rechts und links, wobei Knoten an den äußeren Kanten der Matrix mit korrespondierenden Knoten an der jeweils gegenüberliegenden Kante verbunden sind), mit dem Resultat dass diese ihre Lichtquellen einschalten. Diese von dem Knoten ausgehende Aktivität synchronisiert das gesamte Netzwerk, so dass es oszilliert indem es (vertikal und horizontal) abwechselnde Lichtquellen gemeinsam (zu Zeitpunkten t1, t2, t3, t4, t5, t6...) ein- und ausschaltet. Es weist darüber hinaus zahllose paradoxe Schleifen auf. Die Verbindung der gegenüberliegenden äußeren Kanten der Matrix, sei sie baulich oder rein infrastrukturell ausgeführt, verbindet eine gerade Reihe (Spalte) mit einer ungeraden und eine ungerade mit einer geraden. (Ich habe dieses Netzwerk gebaut und es verhält sich wie beschrieben.)

Die dynamische Stabilität der Aktivität des Netzwerks, die eindeutig komplexer ist als die der in ihm enthaltenen einzelnen Knoten, liefert eine Vielzahl paradoxer Kontexte (alle Möglichkeiten) in denen der Beobachter zwischen gleichzeitig auftretenden Alternativen wählen (unterscheiden) kann:

• Beim Beobachten des Netzwerks (dem Ein- und Ausschalten der Lichtquellen), kann der Beobachter sich auf eine Lichtquelle konzentrieren, die gerade eingeschaltet wurde. Wenn diese erlischt kann er eine ihrer vier Nachbar-Lichtquellen (vier Möglichkeiten) wählen, die soeben eingeschaltet wurden. Dann kann er sich auf die gewählte Lichtquelle konzentrieren und, wenn diese erlischt, eine ihrer vier Nachbar-Lichtquellen wählen, die nun eingeschaltet werden und so weiter ad infinitum. Dabei formt der Beobachter einen von den betrachteten Lichtquellen bestimmten Pfad. Bei jeder Lichtquelle die der Beobachter betrachtet alternieren die vier Nachbarn, als paradoxer Kontext logisch oben, unten, rechts oder links und durchdringen sich paradox oben, unten, rechts und links. (Wie oben in der letzten Abbildung der logischen und paradoxen Toroide dargestellt).
  
  
• Der Beobachter kann sich auch entscheiden der Bewegung einer oder mehreren Diagonalen zu folgen. Während das Netzwerk oszilliert wandern diese Diagonalen hoch in Richtung der linken oberen Ecke und hinunter in Richtung der unteren rechten Ecke. Der Beobachter kann sich auch entscheiden, Diagonalen zu folgen, die in Richtung der rechten oberen Ecke und hinunter in Richtung der linken unteren Ecke wandern. Für den Beobachter der Diagonalen alternieren, als paradoxer Kontext, logisch hoch oder hinunter und sie durchdringen sich paradox zu hoch und hinunter.
  
  
• Dasselbe gilt für die Diagonalen, die aus ausgeschalteten Lichtquellen bestehen, sofern der Beobachter sich entschließt, diesen Diagonalen zu folgen.
  
  
• Der Beobachter kann sich auch entscheiden jede beliebige Gruppe von Lichtquellen (beispielsweise 2, 3, 4 ... n Lichtquellen an) zu beobachten und, durch das Auswählen der Bewegungen jeder betrachteten Lichtquelle Muster formen, aus den Pfaden, die durch alle betrachteten Lichtquellen determiniert werden. In der unteren H&aum;lfte der folgenden Illustration zum Beispiel hat sich ein Beobachter entschieden, eine Gruppe von zwei eingeschalteten Lichtquellen (rot) entlang einer Diagonalen zu folgen. Anschließend wählt der Beobachter für jede der beiden Lichtquellen eine vertikale (horizontale) Bewegung, jedoch in einander entgegengesetzten Richtungen und so weiter, wie durch die Pfeile angezeigt. Während das Netzwerk oszilliert oszilliert dieses Paar, aus Sicht des Beobachters, wie eine Wippe und es rotiert wie eine Windmühle wenn sich vertikale und horizontale Bewegungen ablösen.

(Wenn die Anzahl der gewählten Lichtquellen für jede Gruppe wächst, dann wächst die Anzahl der möglichen, vom Beobachter durch das Auswählen benachbarter Lichtquellen formbarer Muster noch mehr. Dies passiert sogar in einem bescheiden dimensionierten Netzwerk wie dem hier beschriebenen. Beachten Sie, dass der Beobachter nicht sämtlichen möglichen Mustern folgen kann, wodurch ihm unvermeidbar alle Muster, denen er nicht folgt, entgehen, da jeder Beobachter nur soundso viel von seiner Umwelt Aufmerksamkeit schenken kann und den Rest verpassen muss.)

• Und viele andere.
  

Sehen sie Animation.

Sehen sie Animation.

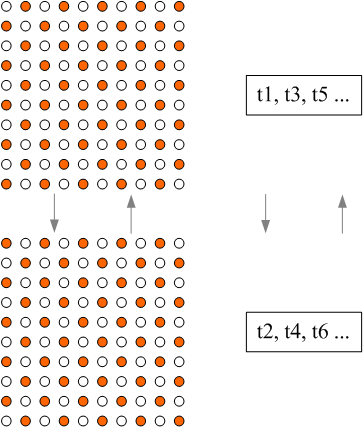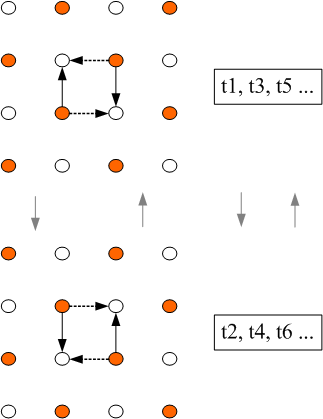Die Auswahlen des Beobachters haben keinen Einfluss auf die Oszillation des Netzwerks, doch ohne die Aktivität des Netzwerks hätte der Beobachter nichts auszuwählen. Andererseits macht die Aktivität des Netzwerks ohne einen Beobachter keinen Sinn.

Durch die Ergänzung des Netzwerks mit Lichtsensoren könnte ein (dem Netzwerk) externes Licht die dynamische Stabilität der Netzwerkaktivität beeinflussen, so dass einige Nachbarn sich nicht wie erwartet einschalten oder umgekehrt. Hierdurch verändert sich die Anzahl der Auswahlen, die dem Beobachter zur Verfügung stehen. Dies zeigt, dass das Netzwerk jede beliebige Form haben kann: regelmäßig, wie hier beschrieben, oder irregulär.

Da das Netzwerk selbst Licht erzeugt, können einige Lichtquellen als Effektoren agieren und mit einem anderen oder dem eigenen Netzwerk interagieren (z.B. mit einem Spiegel).

Für einen Beobachter können einige der Lampen Effektor-Oberflächen, und einige Lichtsensoren können Sensor-Oberflächen des Netzwerks repräsentieren. In einem solchen Netzwerk führt jede Aktivität irgendwo im Netzwerk zu weiterer Aktivität anderswo im Netzwerk, die „externe Umwelt” des Netzwerks inbegriffen.

Eine externe Stimulation (z.B. Licht), die die Aktivität einiger Lichtquellen unterdrückt, kann zur teilweisen oder vollständigen Isolation anderer Lichtquellen führen. Diese werden weiterhin in Isolation oszillieren, doch die Aktivität der Netzwerks wird desintegrieren und aufhören als Einheit zu oszillieren.

Lassen Sie uns nun das Netzwerk oszillierender Lichtquellen als Gesellschaft individueller Organismen (Lichtquellen oder Gruppen von Lichtquellen) beobachten, die mit ihren unmittelbaren Nachbarn interagieren. Unter bestimmten Umständen können diese Interaktionen mit denen einer tatsächlichen Gesellschaft korrespondieren, wie z.B. einem Ameisenhügel, einem Bienenstock oder einer Gruppe von Menschen. Beachten Sie, dass für einen Beobachter, der vom Funktionieren dieser „Gesellschaften” nicht beeinflusst wird, diese „Gesellschaften” keinen Sinn machen außer als oszillierende Netzwerke, die schlicht oszillieren wie die oben beschriebene Matrix von Lichtquellen (egal wie Komplex die Oszillation ist).

Stellen sie sich einen Besucher in einem fremden Land vor, in dem die Einwohner eine Sprache sprechen, die der Besucher nicht versteht und in dem die Einwohner nicht die Sprache des Besuchers verstehen. Eine Zeit lang könnte der Beobachter nicht mit den Menschen des Landes interagieren. Der Besucher verhielte sich also nur als Beobachter der Menschen dort, und umgekehrt, solange keine der Parteien die andere als störend empfindet. Die Gesellschaften oder Gruppen, die der Besucher antreffen könnte, werden ihm solange als schlicht oszillierende Netzwerke erscheinen, bis der Besucher die Sprache lernt und der Oszillation (dem Tanz) beitritt.

Die Aktivität dieser oszillierenden Netzwerke könnte örtliche Beschädigungen erleiden (einige Knoten könnten aufhören zu oszillieren, Stimulations- oder Unterdrückungs-Signale könnten blockiert werden etc.), doch das Netzwerk insgesamt fährt in seinem Tanz fort und lässt dynamische Stabilität und Instabilität einander durchdringen, wodurch das Leben der Gruppe oder der Gesellschaft und ihrer Mitglieder bereichert wird. Durch weitreichenden Schaden könnte die Aktivität des Netzwerkes desintegrieren.

Beachten Sie, dass sich die Aktivität (Oszillation) im Netzwerk insgesamt selbst aufrecht erhält, da jeder Aktivität irgendwo im Netzwerk zu weiterer Aktivität (integriert, synchronisiert) anderswo im Netzwerk führt - Aktivität, die durch viele mögliche paradoxe Rückkopplungs-Schleifen zu der ursprünglich betrachteten Aktivität wiedereintritt. (Ein Kreis, eine Kugel, mit Mittelpunkt überall und seinem Umfang, Oberfläche nirgendwo).

Es sollte durch das oben Diskutierte klar werden, dass die ursprüngliche 2D-Vernetzung von Knoten in eine multidimensionale Vernetzung von Knoten wachsen könnte, dass die Aktivität von Knoten wesentlich komplexer werden können als das Ein- und Ausschalten einer Lichtquelle und dass die Signale zwischen den Knoten ebenso an Komplexität zunehmen können. Lebende Organismen, zum Beispiel, interagieren durch eine Vielzahl von Signalträgern und komplexer Signale: elektrochemische, chemische, Licht, Ton, Tanz etc. ... und, selbstverständlich, menschliche Sprache.

Die folgende Abbildung repräsentiert die Zeitpunkte (t1, t2, t3, t4, t5, t5, t6, ...) eines Knoten (im Zentrum), seine Nachbarn und die Nachbarn seiner Nachbarn in einer multidimensionalen Vernetzung von Knoten. Wie zuvor „schalten” sich, wenn sich ein Knoten „ausschaltet (weiß)”, all seine Nachbarn (ein „rot”). Wenn n=4 repräsentiert die Abbildung eine 4-D (D1, D2, D3, Dn) Vernetzung von Knoten mit je 8 klar gekennzeichneten Möglichkeiten. (Wenn Dn Zeit repräsentiert, so könnte die Abbildung eine 4-D Raum-Zeit Mannigfaltigkeit repräsentieren.) (Ich habe dieses Netzwerk gebaut und es verhält sich wie beschrieben.)

Sehen sie animation.

(Eine 1-D (eindimensionale) Vernetzung von Knoten bietet einem Beobachter einen paradoxen Kontext mit 2 Möglichkeiten an jedem Knoten (2 Nachbarn); eine 2-D Vernetzung von Knoten, wie die, die wir zuvor diskutiert haben, bietet an jedem Knoten 4 Möglichkeiten (4 Nachbarn); eine 3-D bietet 6; eine 4-D bietet 8; und eine n-D bietet 2n Möglichkeiten. (Eine 0-D bietet keine).)

Um sich mehr als vier Dimensionen vorzustellen, muss sich der Leser die zusätzlichen Knoten und deren Verbindungen zum Knoten im Zentrum zwischen D3 und Dn und zwischen –D3 und –Dn vorstellen oder zeichnen, wie in der Abbildung angedeutet.

Trotz dieser Zunahme an Komplexität oszilliert ein unbehindertes Netzwerk individueller Elemente nach wie vor, ungeachtet der Komplexität ihrer Knoten, der Signale oder ihres beobachteten Verhaltens sowie ungeachtet der Anzahl an Dimensionen in denen sich ihre Interaktionen entfalten.

Die essenziellen Eigenschaften des 2-D Netzwerks haben sich nicht geändert: es kann jede Form annehmen, seine Aktivität hat keine Grenzen, jede Aktivität führt zu weiterer integrierter Aktivität. Es hält lokalen und temporären Schäden stand, es kann mit anderen ähnlichen Netzwerken interagieren und weitreichender oder permanenter Schaden kann die Netzwerkaktivität als oszillierende Einheit zur Desintegration führen.

Wenn Ameisen ihre „Sprache” (Signale zwischen den Knoten) verlieren, dann desintegriert die Aktivität des Ameisenhügels als Einheit. Dasselbe wird Bienen und ihrem Bienenstock passieren. Und so wird es allen sozialen Organismen (Menschen eingeschlossen) und ihren Gesellschaften passieren, wenn sie ihre „Sprache” verlieren.

Beachten Sie jedoch, dass für eine komplexe Menge an Knoten wie etwa Menschen in einer Gesellschaft eine präzise und/oder begrenzte „Sprache” wie zum Beispiel die der Ameisen oder Bienen bereits einen Verlust darstellt. Ein komplexes Individuum, das an sich bereits eine Einheit darstellt und nicht vollkommen einer Gesellschaft unterworfen ist (so wie eine Ameise in einem Ameisenhügel, eine Biene in einem Bienenstock etc.), benötigt eine Gemeinschaft komplexer Individuen, die mit der Reichhaltigkeit und Flexibilität interagiert, die notwendig ist, um das bestmögliche Leben für jedes Individuum in der Gemeinschaft zu erreichen und zu erhalten.

Unglücklicherweise organisieren sich menschliche Gesellschaften in rigiden Hierarchien, die die Vorhersehbarkeit (Trivialität) ihrer Mitglieder benötigt, die somit rapide die Reichhaltigkeit und Flexibilität ihrer Interaktionen verlieren, und sie zu trivialem Sprechen erniedrigt, das nicht anders ist als die „Sprache” von Ameisen oder Bienen. Eine Gesellschaft kann sich entwickeln, doch keine menschliche.

Hierarchien ersetzen Denken und Konversation mit Ritualen, seien sie säkular oder religiös, so dass weder Denken noch Konversation stattfindet. Dies bringt Gesellschaften hervor, denen die Gegenwart unbehaglich ist, mit Sehnsüchten für eine primitive Vergangenheit und Vorahnungen einer Zukunft ohne Menschen.

Ein Entspannen der willkürlichen Unterscheidungen, die nötig sind um hierarchische Gesellschaften zu etablieren und zu erhalten, in ausreichendem Maß dass Hierarchien eliminiert werden, wird dementsprechend der Reichhaltigkeit und Flexibilität von Interaktionen erlauben sich zu erholen und wieder aufzublühen.

Vergegenwärtigen Sie sich das Netzwerk von Oszillatoren als eine Gemeinschaft von Beobachtern mit einer nicht-hierarchischen Aktivität. Vergegenwärtigen Sie sich die Störungen, die diese Aktivität beeinflussen, ohne sie zu desintegrieren, die jedoch Stimulationen für unvorhersehbare Konflikte darstellen. Die Flexibilität der nicht-hierarchischen Aktivität gestattet dem Netzwerk, permanente Konflikte in einen neuen Tanz (Oszillation) einzubeziehen oder Konflikten standzuhalten und seinen ursprünglichen Tanz wiederherzustellen.

Eine nicht-hierarchische Gemeinschaft individueller Beobachter benötigt keine rigiden Unterscheidungen und wird daher ansonsten unlösbare Konflikte bewältigen.

Paradoxes Denken

Dem logisch denkenden Beobachter sind Paradoxe unangenehm. Dieser Beobachter, der von vornherein die meisten Möglichkeiten ausschließt, hält Paradoxe für fehlerhaftes Denken. Daher zieht ein logisch denkender Beobachter „logisches Denken” oder „paradoxes Denken” in Betracht.

Für einen paradox denkenden Beobachter zählen alle Möglichkeiten und alle Möglichkeiten durchdringen einander. Für einen paradox denkenden Beobachter durchdringen sich folglich „logisches” oder „paradoxes” zu „logischem” und „paradoxem” Denken.

Ein lebender Organismus produziert und erhält sich selbst als geschlossenes paradoxes Netzwerk von Prozessen und Komponenten, das sich selbst als Beobachter einer Umwelt unterscheidet, der von eben dieser Unterscheidung hervorgebracht wird.

Ein lebender Organismus, als eine Zelle oder als ein mehrzelliger Organismus, benötigt zum Überleben eine geeignete Umwelt. Er kann auch die Rolle eines Prozessors spielen der, mit anderen ähnlichen Organismen interagierend, einen Teil einer geschlossenen Kette von Prozessoren darstellen kann, der, auf der Basis einer gegebenen oder selbst hergestellten geeigneten Umwelt, zu einem neuen lebenden Organismus aus lebenden Organismen führen kann. Zum Überleben muss dieser neue Organismus eine geeignete Umwelt für das Überleben seiner konstituierenden Organismen sowie für deren Ersetzen, sei es durch Reproduktion oder auf andere Weise, bereitstellen. Diese neuen Umstände erfordern, dass die konstituierenden Organismen, wie von dem neuen Organismus gefordert, ihre Unvorhersehbarkeit (ihr paradoxes Denken) zugunsten ihrer Vorhersehbarkeit (ihres logischen Denkens) aufgeben.

Dies geschieht zum Beispiel Ameisen und Bienen, wenn sie sich dem Ameisenhügel oder dem Bienenstock, dem neuen lebenden Organismus, unterordnen.

Lassen Sie uns kurz zur Metapher des Netzwerks aus Oszillatoren zurückkehren. In Isolation oszilliert jeder Knoten uneingeschränkt, befähigt durch seine interne paradoxe Schleife. Als Teil eines Netzwerks muss er jedoch, so wie es die Logik des Netzwerks verlangt, entsprechend den von anderen Knoten empfangenen Signalen, seine Oszillation mit anderen Knoten im Gleichschritt halten.

Die Aktivität eines Nervensystems benötigt, so wie die anderer Netzwerke, das Vorhandensein miteinander verbundener Oszillatoren (in diesem Fall ein oder mehrere Neuronen innerhalb einer oder mehrerer paradoxer Schleifen), die diese Aktivität generieren und aufrecht erhalten. Auf diese Weise bilden die Neuronen ein Netzwerk aus Oszillatoren, das als Nervensystem bezeichnet wird. Anderenfalls würde die Aktivität des Nervensystems verschwinden und mit ihr die vielen Möglichkeiten, die es lebenden Organismen bietet.

Die dreidimensionale Struktur des Nervensystems enthält unzählige Neuronen mit unzähligen Verbindungen. Da jedes Neuron mit vielen weiteren Neuronen verbunden ist, funktioniert das Nervensystem, ungeachtet seiner dreidimensionalen Struktur und unabhängig von der Position von Neuronen und von den Einschränkungen von 3D-Raum, auf multidimensionale Weise. Dies eröffnet ihm das enorme Potential eine Vielzahl von Pfaden zu aktivieren, inklusive denjenigen Pfaden, die durch das Involvieren von Effektoren und Sensoren die Umwelt mit einbeziehen, kurzum alle Möglichkeiten - so wie in einem paradoxen Kontext in dem ein Beobachter vorläufige Unterscheidungen trifft, wie es für das Interagieren mit sich selbst und mit der Umwelt erforderlich ist. Sensoren und Effektoren bieten eine erste vorläufige Unterscheidung: Der Beobachter unterschieden von seiner Umwelt, in der sie selbst und andere Beobachter existieren.

Ein Beobachter mit einem Nervensystem das potentiell so komplex ist wie das eines menschlichen Kleinkindes, tritt in eine Welt ein, die bereits von anderen menschlichen Beobachtern bewohnt und geformt ist.

Das Nervensystem von Kindern entwickelt sich durch Interaktionen mit ihren Umgebungen und mit sich selbst, in denen sie alle Möglichkeiten in Betracht ziehen, inklusive Emotionen, Empfindungen und andere Beobachter, wobei von seinen Effektoren und Sensoren voller Gebrauch gemacht wird.

Die Aktivität des kindlichen Nervensystems bietet einen paradoxen Kontext (alle Möglichkeiten), in dem sich ihr paradoxes und logisches Denken entwickeln.

Andere Beobachter, einige gleichgültig, einige fürsorglich, werden die Welt-Erkundung der Kinder anleiten. Einige werden ihr logisches Denken mit einer begrenzten Sichtweise stimulieren, andere werden ihr paradoxes Denken mit all seinen Möglichkeiten stimulieren. Viele werden versuchen, sie darin zu instruieren, wie sie die Welt sehen. Alle werden die Kinder beeinflussen und damit in unterschiedlichem Maß Erfolg haben.

Ein Kind das Glück hat wird sich sein paradoxes Denken lebendig erhalten und wird dementsprechend in einem paradoxen Kontext alle Möglichkeiten in Betracht ziehen, indem es durch unabhängiges Denken soweit wie nötig vorläufige Unterscheidungen trifft. Dies wird zu einem Nervensystem führen, das seine ursprüngliche Neugierde, Wissbegierde und Fähigkeit eigenständige Gedanken zu haben für das ganze Leben dieses menschlichen Beobachters erhält. Ein solcher Beobachter wird die menschliche Gesellschaft nicht als Selbstverständlichkeit hinnehmen und bedacht und ohne vorgefasste Ideen, Vorurteile oder Dogmen, welche nur aus logischem Denken hervorgehen, zu dessen Verbesserung beitragen.

Ein Kind das weniger Glück hat wird sein paradoxes Denken zugunsten von logischem Denken unterdrücken und ein Nervensystem entwickeln, das seine ursprüngliche Neugierde, Wissbegierde und sein unabhängiges Denken verlieren wird. Dieses Kind wird bestenfalls zu einem gleichgültigen Mitglied der Gesellschaft heranwachsen, das den Nachwuchs instruiert anstatt ihn zu bilden. Eine bedauernswerte Gesellschaft, von der die meisten Mitglieder in logischem Denken versunken sind, wird dem Wiedereintreten erliegen das bereits im Vorwort erwähnt wurde.

Bald nach ihrer frühen Kindheit entwickeln Menschen auch die Fähigkeit ihre eigenen Aktionen und Gedanken zu reflektieren. Eine bedauernswerte Gesellschaft unterdrückt diese Entwicklung durch beliebige Hierarchien, die die Möglichkeiten des Nervensystems beschränken, so dass bald all ihre Mitglieder diese Fähigkeit verlieren und vollkommen ignorant gegenüber diesem Vakuum in anderen und in sich selbst leben.

Anstatt sich auf logisches Denken und auf die Suche nach einer „Wahrheit” zu verlassen, schlägt der Tractatus vor, sich auf paradoxes Denken und auf die Erkundung aller Möglichkeiten zu verlassen, wodurch logisches Denken in einem neuen Licht erscheint.

So wie bei allen Paradoxen kann kein Beobachter den Tractatus oder einzelne Propositionen darin ohne Trivialisierung und Verlust „erklären”. Die Propositionen des Tractatus sagen, lehren oder erklären nichts; sie zeigen. Sie laden Beobachter ein, der Bequemlichkeit der Trivialisierung zu entkommen, mittels Bildung Alternativen zu erkunden und zu vermehren, Paradoxe und Logiken einander durchdringen zu lassen und instruierten Unterscheidungen zu entkommen. Diese Einladung anzunehmen erfordert Mut, da der Tractatus viele gelobte Begriffe und Gewohnheiten zerstört, und sich von gegenwärtiger „Zivilisation”, Lebensweise und Sprache entfernt.